MULTI-OBJECTIVE OPTIMIZATION
BALANCING CONFLICTING DESIGN OBJECTIVES
Many engineering challenges require dealing with multiple objectives instead of a single objective. As some of the objectives may be (partially) conflicting, the design optimization effort becomes more complex. In most cases, multi-objective optimization need specific trade-offs to be made between various criteria to balance conflicting design objectives and work toward a satisfactory optimal design configuration.
Building a Pareto front
Multi-objective Optimization (MOO) algorithms allow for design optimization taking into account multiple objectives simultaneously. Each objective targets a minimization or a maximization of a specific output.
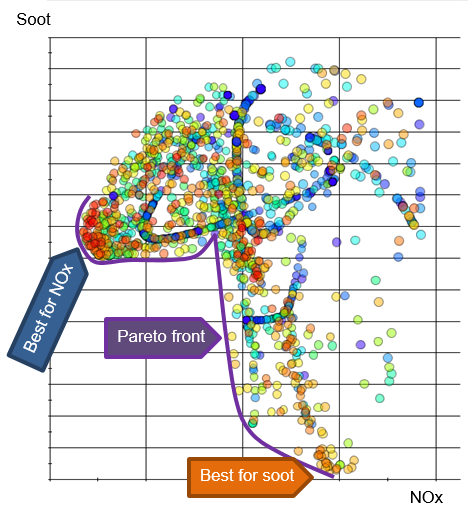
MOO methods search for the set of optimal solutions that form the so-called Pareto front. The outer boundary of this collection of non-dominated points defines the limit beyond which the design cannot be further improved - bordering the region of feasible solutions. Moving along the Pareto front, all the optimal trade-off solutions of the multi-objective problem can be found.
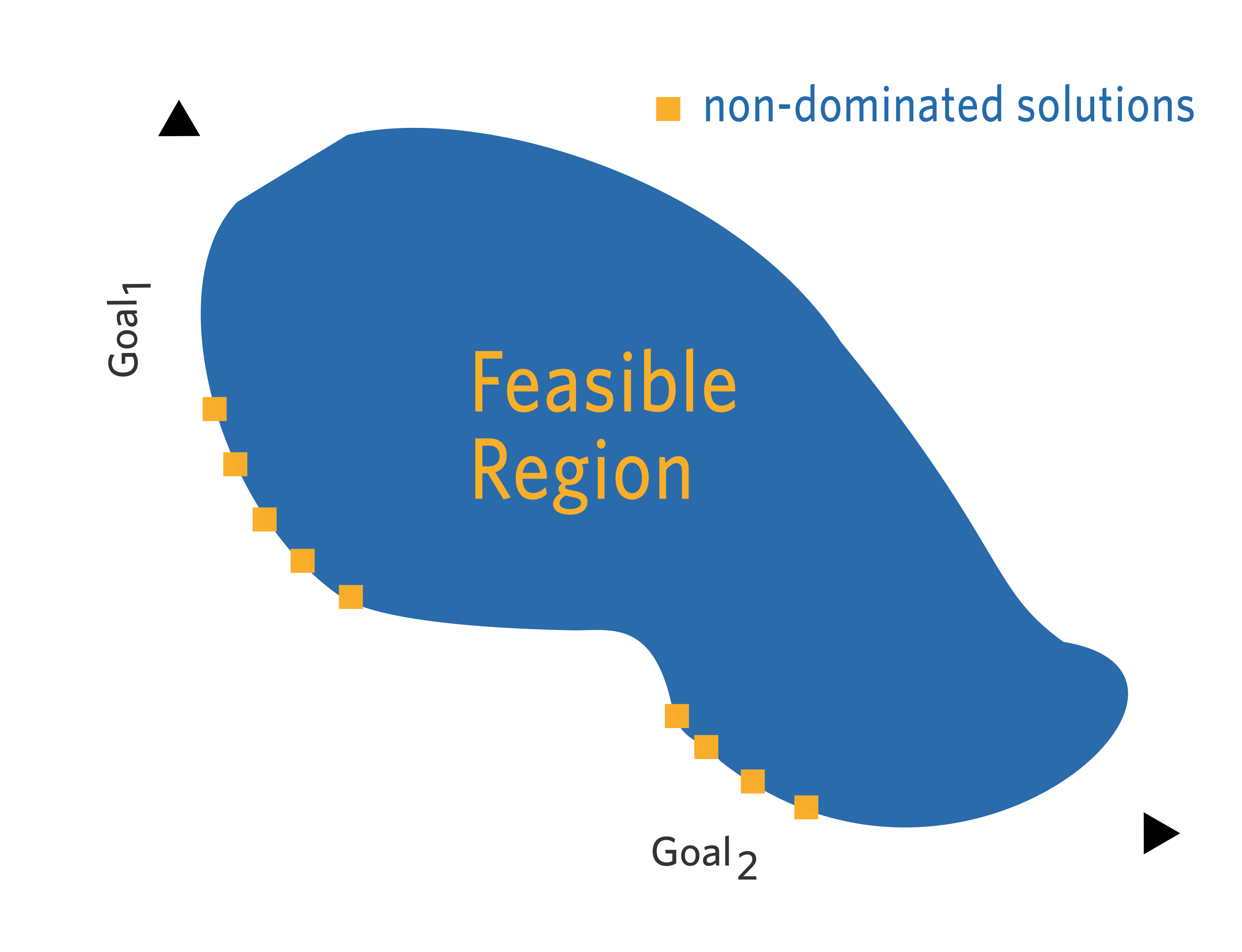
Pareto optimal methods
Ultimately, the decision for the preferred trade-off solution along the Pareto front depends on additional subjective information which has to be judged by the engineering team in charge.
Therefore the real purpose of multi-objective design optimization is identifying the full set of Pareto optimal solutions, rather than finding a single optimal design that outperforms all others (and which doesn’t really exist, by the way). It’s then up to human decision makers to evaluate and quantify all promising trade-offs between the different design objectives.
This trade-off analysis is essentially a subjective decision-making process, requiring a high degree of interactivity with the optimization process. Our state-of-the-art global optimization algorithms (including Differential Evolution, Self-adaptive Evolution, Simulated Annealing, Efficient Global Optimization, Particle Swarm Optimization and Covariance Matrix Adaptation Evolution Strategy) support this kind of process, as they have been developed explicitly to solve general constrained optimization problems.
Pareto point methods
Pareto point methods aim at searching for a single compromise solution between the various objectives. Such trade-off methods convert a multi-objective optimization problem into a single-objective problem. One strategy is to sum up all the objectives in weighted utility function, another way is to select one objective as the primary goal while treating all the others as constraints. Other hierarchical methods rank the objectives in a descending order of importance, and each objective function is then minimized individually. These methods may be fast and efficient, but not all the Pareto optimal solutions can be obtained.

OPTIMIZING FOR THE REAL WORLD
Discover how »©2024 Noesis Solutions • Use of this website is subject to our legal disclaimer
Cookie policy • Cookie Settings • Privacy Notice • Design & Development by Zenjoy