DESIGN OF EXPERIMENTS
SAMPLING THE DESIGN SPACE UP-FRONT
To enhance product performance and engineer products that outsmart competition, engineer teams require profound design space knowledge to help them fully understand the engineering potential. Design Of Experiments (DOE) technologies allow them to efficiently sample the design space by defining and executing a set of optimally chosen virtual or physical prototyping experiments. Combined with our workflow automation technologies, this helps them save considerable amounts of time in the product development process.
Acquiring deeper insights
A Design of Experiments approach starts from the engineering objectives to be addressed, and considers the design factors that can have an impact on these objectives. A detailed plan is laid out and defines the engineering experiments to be run. This plan carefully selects experimental designs so as to maximize the amount of relevant engineering information that can be obtained for a given number of experiments. As it replaces a manual trial-and-error process, this approach paves the way for acquiring the most relevant design space information with minimum computational effort.
Orthogonal & Random Designs
Over time, many DOE methods have been developed that altogether cover a wide range of different applications. In general, these DOE methods can be classified into two categories: orthogonal designs and random designs.
Orthogonal designs are characterized by design factors that are statistically independent and can thus be varied independently from each another. Widely used methods cover so-called fractional and full-factorial designs, central composite designs, and Box-Behnken designs.
With random designs, design factor values are assigned on the basis of a random process. The most commonly used random DOE method is the so-called Latin Hypercube Design (LHD).
Advanced Space-filling Designs
Minimax and Maximin DOE methods optimize the selection of experiments within the design space. Both criteria guarantee better overall coverage compared to optimized Latin Hypercube methods.
While the Minimax method minimizes the maximum distance between any point within the design space and its closest design point, the Maximin method maximizes the minimum distance between each pair of points in the design space. The optimal and robust Minimax and Maximin designs gained through this approach provide a good starting point for engineers, who can be confident they are looking at complete and accurate information on the total design space, including border areas.

Adaptive Methods
Adaptive DOE methods actively exploit design space knowledge being built up as experiments run. This active learning process automatically adds additional experiments whenever and wherever needed to better capture the (originally unknown) design space. This eliminates the risk to undersample the most relevant design space regions (overlooking critical information) or oversample less relevant regions (wasting simulation resources). Our Adaptive DOE technologies offer the flexibility to stop the active learning process at any time, for instance when the required sampling accuracy is reached and/or when the allocated time budget is spent.
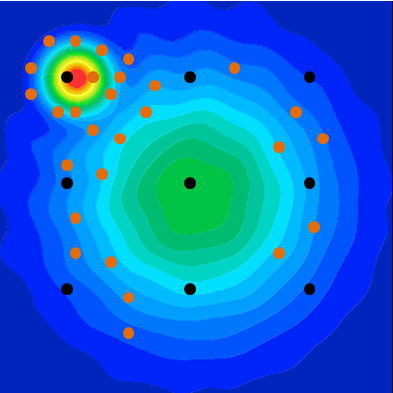
Use of DOE Results
The data collected through DOE methods provide the basis for further post-processing methods & response surface modeling (RSM). Correlation plots, for example, enable engineers to evaluate the relative importance of various design parameters, and zoom in on the most relevant ones. Self-organizing Maps (SOM) generate a color pattern for each design parameter and simulation response. By graphically comparing these individual ‘blueprints’, engineers instantly discover correlations that allow them to fine tune their design optimization strategy or detect design space regions of specific interest.

CONDENSING COMPLEX ENGINEERING PROCESSES
Discover how »©2025 Noesis Solutions • Use of this website is subject to our legal disclaimer
Cookie policy • Cookie Settings • Privacy Notice • Design & Development by Zenjoy