NUMERICAL OPTIMIZATION
WORKING TOWARD THE BEST
Mathematical optimization methods efficiently trace the extremes of a function, through an intelligent arrangement of evaluations. Traditionally, engineers start from a set of design parameters. When manually trying to improve the design, they judge the impact of these parameters on possibly conflicting engineering objectives, such as minimum weight, minimum cost and maximum product performance. With our numerical optimization technologies, that entire process is reversed – enabling engineering teams to work their way back from design targets to the appropriate design parameter values.
Numerical optimization methods
When focusing on numerical optimization methods, there is a choice of local, global and hybrid algorithms. Local optimization methods search for an optimum based on local information, such as gradient and geometric information related to the optimization problem. Similarly, global optimization methods – usually probability based – use global information and offer a high probability of finding the global optimum. Hybrid optimization methods combine the local and the global approaches in a seamless strategy, typically relying on response surface approximation to find a global optimum with minimum effort. Any in-house developed optimization methods (whether local, global or hybrid) can easily be embedded thanks to methods integration technologies.
Local Optimization Methods
Our robust set of local optimization algorithms include NLPQL, Sequential Quadratic Programming (SQP), Generalized Reduced Gradient (GRG) and Adaptive Region Method (ARM Order 1 and 2). These algorithms are useful for solving general constrained optimization problems, and typically converge quickly to a local optimum. They require the definition of an objective function, the boundaries for the input parameters, and if needed a set of constraints for the outputs. Sensitivity-based algorithms use gradients of the objective function as well as the constraints, to efficient identify a local optimum.
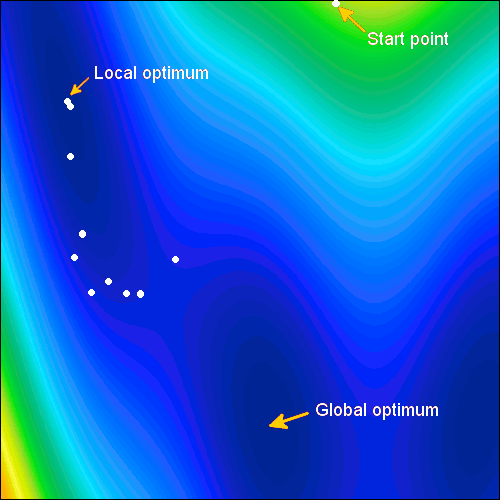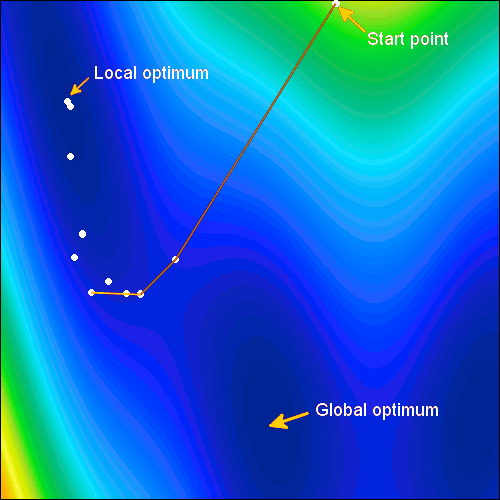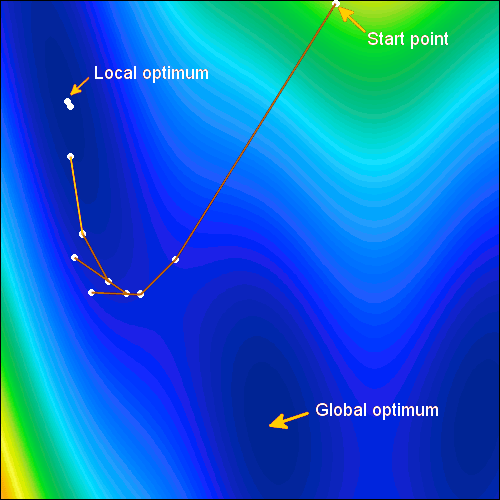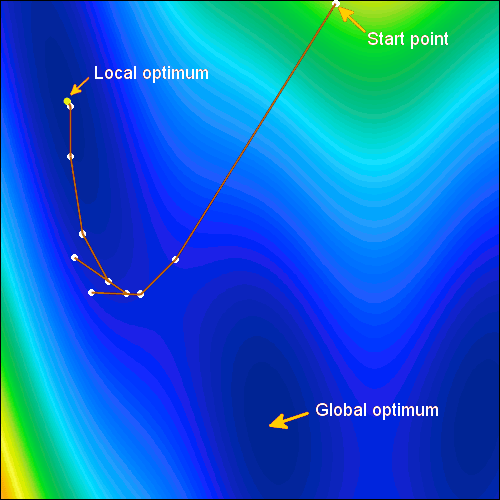
Global Optimization Methods
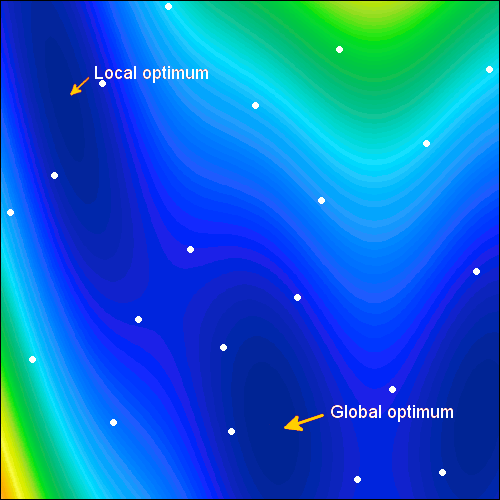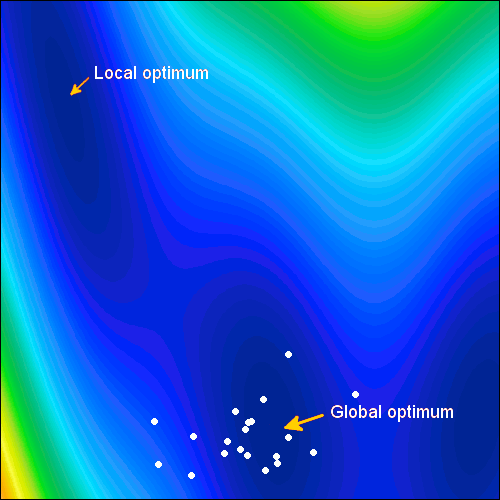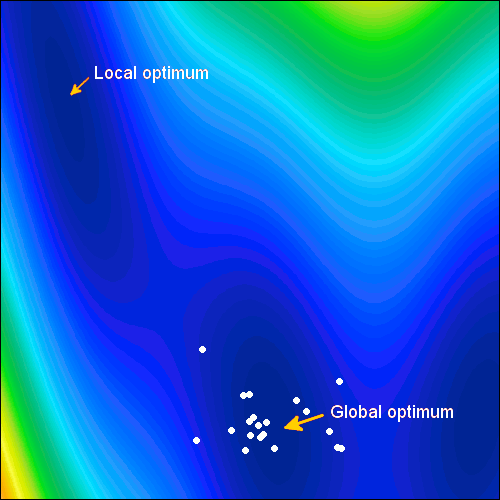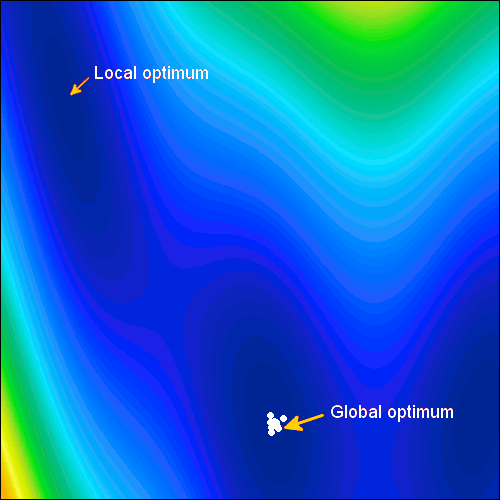
Our state-of-the-art global optimization algorithms include Differential Evolution (DE), Self-adaptive Evolution (SE), Simulated Annealing (SA), Efficient Global Optimization (EGO), Particle Swarm Optimization (PSO) and Covariance Matrix Adaptation Evolution Strategy (CMA-ES). These algorithms have been developed to solve general constrained optimization problems. Whereas local optimization algorithms target a local optimum, global optimization algorithms offer a high probability of finding a global optimum. This can achieve this by looking around in the design space at multiple locations simultaneously.
Adaptive-Hybrid Methods boost efficiency
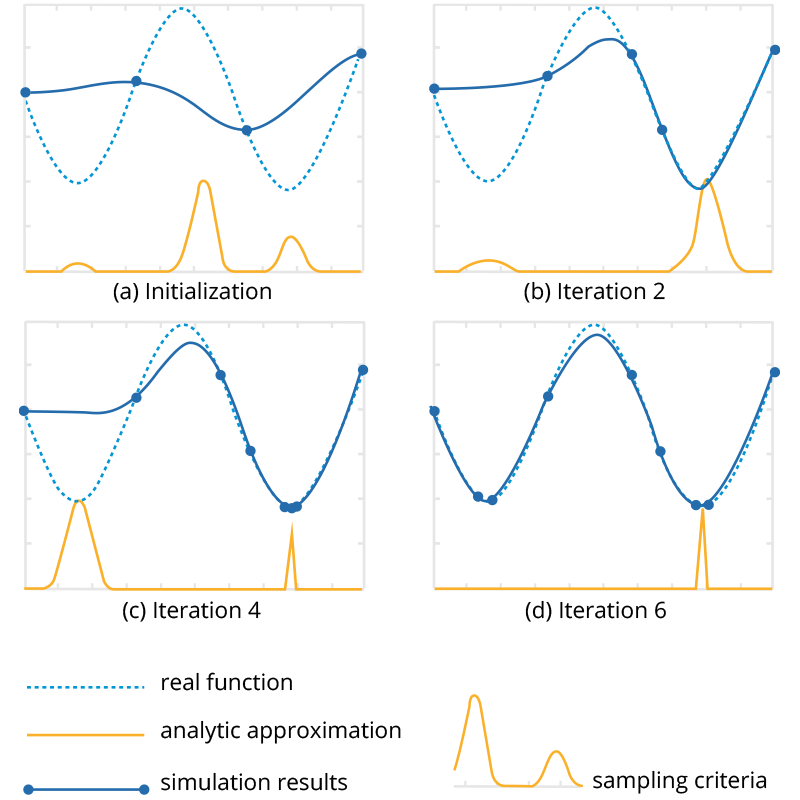
Adaptive region optimization (ARM Order 2) and the Efficient Global Optimization (EGO) methods are developed as an extension to the response surface model (RSM) technology. By taking advantage of the response surface, the location of the optimal point can gradually be searched. With every approximation step the resolution of the response surface becomes finer, helping the algorithm to locate an optimum design.
BALANCING CONFLICTING ENGINEERING OBJECTIVES
Discover how »©2025 Noesis Solutions • Use of this website is subject to our legal disclaimer
Cookie policy • Cookie Settings • Privacy Notice • Design & Development by Zenjoy