ROBUST OPTIMIZATION
OPTIMIZING FOR THE REAL WORLD
Engineering simulation is a typical example of a deterministic process. For a given set of input variables, the corresponding outputs are always identical. This is entirely different in the real world however, where input variables may vary slightly as a result of manufacturing tolerances and geometric properties.
Ensuring a robust design
Due to the variability of the input variables, the outputs are usually no fixed values but rather correspond to a range of values distributed around a mean value. To avoid that even slight variations of the design parameters negatively impact the expected product quality, Robust Optimization takes design parameter variability into account and subsequently applies robustness concepts and methods to ensure a robust design. With robust designs, the number of product recalls and repairs drops drastically – resulting in major savings and a better market reputation.
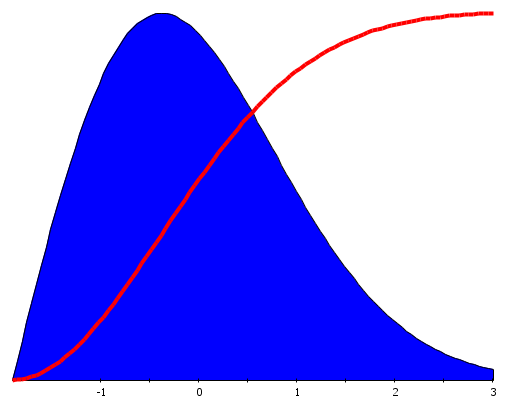
Robustness-based optimization methods
In such an optimization scheme, a measure for the robustness of the system or component is used as optimization constraint or objective in order to meet the best robust performance possible. This optimal solution is insensitive to small design changes so that if small perturbations of the design parameters occur, the performance of the system or component does not drop below the desired quality level.
As all of our robustness assessment methods (Monte Carlo, First-Order Second-Moment, etc.) can be used for optimization purposes, robust design capabilities become an integral part of the engineering simulation process.
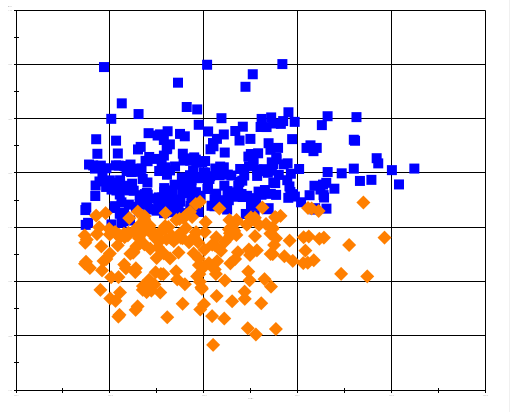
Taguchi robust design
Genichi Taguchi, a Japanese engineer, published his first book on experimental design in 1958. His methods have earned him the most well-known ‘brand’ in the field of design of experiments. The aim of the Taguchi design is to make a product or process more stable in the face of variations over which we have little or no control, for example, making sure that an engine can perform reliably under different ambient temperatures.
Taguchi methods separate design variables into control factors and noise factors. Control factors are the variables that can be practically and economically controlled, such as dimensions, material parameters, etc. Noise factors are variables which are difficult or expensive to control in practice, although they can be controlled in an experiment (such as ambient temperature, etc.) The objective is to determine the combination of control factor settings that will maximize the product’s robustness to the expected variation in the noise factors.
DELIVERING A HIGHER DEGREE OF CONFIDENCE
Discover how »©2025 Noesis Solutions • Use of this website is subject to our legal disclaimer
Cookie policy • Cookie Settings • Privacy Notice • Design & Development by Zenjoy